1. Introduction

The goal of Knowledge Representation is to build formal representations of the knowledge of domain experts. There are many different kinds of knowledge that could be considered, but we focus on knowledge that distinguishes good situations from bad situations. Some examples:

• A production schedule in a factory links machines to tasks and time slots. A good schedule avoids scheduling two different jobs on the same machine at the same time, makes sure that each job is scheduled on the right kind of machine, etc.
• A robot's plan of action assigns actions to a number of time points. A good plan is such that each action can actually be executed at the time it is planned.
• A move in a board game updates the position of some of the game pieces. A good move does this in a way that respects all of the rules of the game.
• A product configuration consists of a number of components that can be manufactured from different materials and that can be linked together in different ways. A good configuration uses matching components in such a way that the customer's requirements are all met.

Once we know what distinguishes good situations from bad situations, we can perform a number of useful inference tasks, such as:

• Find any/all good situations that exhibit a certain property. For instance, find a feasible plan of action for a robot that achieves the robot's goal.
• Find the "best" good situation that exhibits a certain property. For instance, given the current position of a board game, find the valid move that yields the most points.
• Decide if a given situation is good or bad. For instance, validate that a proposed product configuration is indeed valid.
• Find properties that are shared by all good situations. For instance, find out if all valid product configurations must contain a certain kind of component.

The IDP-Z3 system allows to perform a number of such inference tasks on knowledge that is expressed in the FO(·) language.

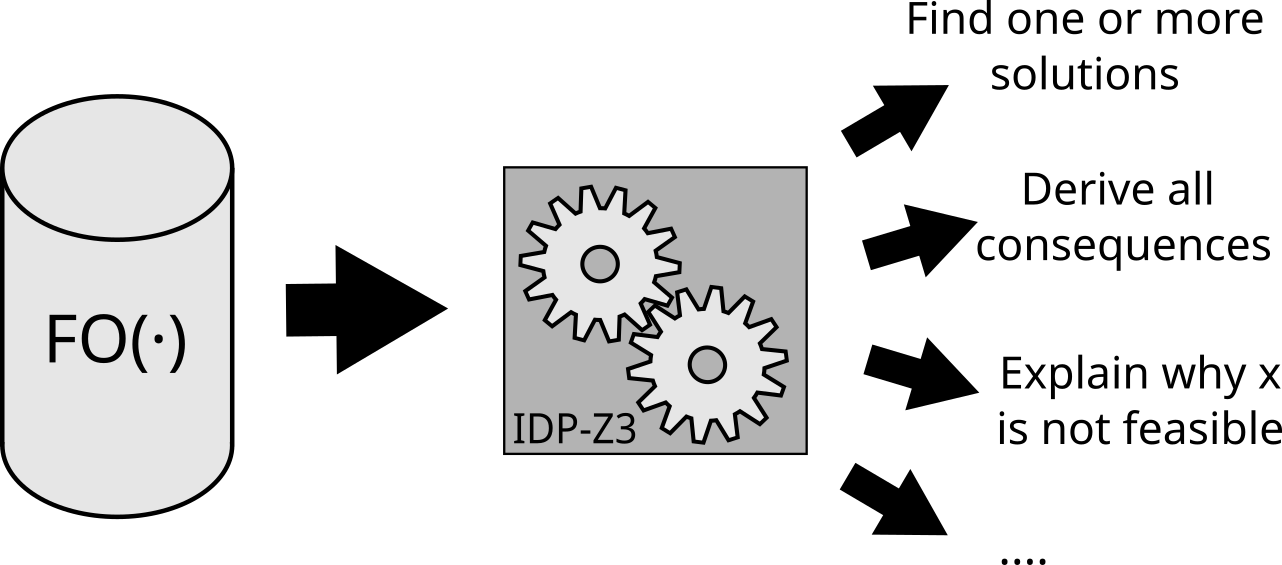
To represent this kind of knowledge, we need to do two things:

1. Define what a "situation" precisely is.
2. Exhaustively enumerate the properties that distinguish good from bad situations.

FO(·) is an extension of classical first-order logic (FO) and it borrows classical logic concepts to accomplish these two tasks:

1. A situation is represented by a structure for a given vocabulary. To define the set of all possible situations, we therefore have to decide on a vocabulary.
2. A property of such a situation is represented by a formula in the given vocabulary. To distinguish good from bad situations, we must therefore write a theory, i.e., a set of formulas.

We now address both topics separately.